I found the opening chapter in Part III, "Having a Body" to be the most interesting one yet. Part I gives us an initial idea of the concept of the fold and a tangible image to guide us. The fold is a fractal structure that ends up confusing two topologically distinct sides, just as it would be hard to distinguish the inside and outside of a fabric folded over on itself again and again to produce folds within folds.
Part II explores the way the fold of the 'concave' or 'spiritual' side can then include an infinity of sub-folds. This leads us all the way to the central concept of the monad, a spiritual 'unit' that includes or enfolds the whole world. Given the centrality of the monad in Leibniz's philosophy, we might be tempted to classify it as a type of atomist idealist. After all, the monad seems to be modeled on the conscious unity of the human subject. To some extent this is accurate, but we should be aware of the ways in which the marriage of idealism and atomism already produces a unique flavor of both. Many of the monads are not what we would recognize as minds -- it's not just humans who are monads -- nor are the ones we would recognize treated as purely simple structures without an interior -- in contrast to the atom, the monad has an infinitely nested interiority. Still, the natural question for any flavor of idealism is why it seems like we also have a body. If the substance of reality is ideal or spiritual, does this make the body an illusion, a mere appearance? Why do we need a body at all?
In Part III, Deleuze answers this question beautifully and profoundly, in a way that leads him to a full expression of the concept of the fold in the final pages of the chapter. The short version is that the structure of Leibniz's peculiar idealism, with its infinitely folded units, drags the body along with it, almost as a byproduct. Once Leibniz delves into the folds of the soul, he cannot stop there but is forced to keep going.
The whole question is one of knowing whether, in assuming the force to engender the perceived and the unity of the perceived in the monad, Leibniz does not also assume the force to engender bodies outside of the monads, and outside of their perceptions. (F, 122)
The spiritual folds within folds of the concave side are necessarily 'filled' by the matter of the convex side. There is only one fold, but it must always have two sides which match or correspond to one another and move together in perfect synchrony. The fractal enfolding of the spirit is the same action as the infinite infolding of matter, the push of one matched by the pull of the other. In a sense, we might consider this the Leibnizian version of Spinoza's mind-body parallelism, even though the image is completely different. Here the two sides are completely inter-penetrated, each following every baroque inflection of the other's curve. But they never touch.
As you might suspect, the long version is quite a bit longer. Deleuze phrases the whole thing as "deduction" of why the monad requires a body. So the starting point is the detailed understanding of the monad that he developed in chapter 5. There, we saw that the monad was a composition of a set of primitive singularities or ideal events -- predicates not attributes. We should note that this simple starting point already hides a dizzying complexity. Monads are unities, but they are not simple or without 'parts'. They presuppose the world as a "pure emission of singularities" including the particular primitive singularities from which they are built or which they condense. Here, to give an example, are the singularities of the biblical Adam.
There is an antecedence of the world in relation to the monads, even though a world does not exist outside the monads that express it. But God does not first of all create Adam, even if he makes him sin, or perceives [s'apercevoir] that he will sin: he creates the world in which Adam sins, and includes in the world all the individuals that express it (Sextus raping Lucretia, Caesar crossing the Rubicon ...). We start from the world as a series of inflections or events: it is a pure emission of singularities. Here, for example, are three singularities: to be the first man, to live in a garden of paradise, to have a woman emerge from one's side. And then a fourth singularity: to sin. Such singularities-events are in relation with "ordinary" or "regular" points (the difference here matters little). A singularity is surrounded by a cloud of ordinaries or regulars. (F, 83)
We presume that, in each case, a singularity can be prolonged to the neighborhood of other singularities, along regular lines that have common values in both directions. But here is a fifth singularity: to resist the temptation. It is not simply that this singularity contradicts the fourth one, "to sin," such that a choice must be made between the two. It is rather that the lines of prolongation that go from this fifth point to the three others are not convergent, that is, they do not pass through common values: it is not the same garden, nor the same primeval world [priméité], nor the same gynegenesis. There is a bifurcation. (F, 84)
But at the same time, these other singularities are nothing but the traces of other monads that compose the same compossible world. The world does not actually exist as a thing in itself outside the monads. But the monads are all made by God for this single convergent world. The world is woven of monads, but each thread in the fabric contains all the others as strands within it. As with Indra's Net, every thing is everything.
Everything is connected, but not in any order. Each monad includes the entire world, but ordered according to a particular point of view. It contains all the singularities that the world emits, but it only condenses a certain subset of these. Their relation constitutes the defining characteristic that makes each monad a distinguishable individual despite the fact that they all include the same world in its entirety. The joining of this particular set of primitive singularities into a continuity is what Deleuze calls their "condensation" (to refer to the idea of a phase transition which lurks beneath the surface here). Each singularity is a point capable of being prolonged to the neighborhood of another singular point in precisely the way a point of inflection is 'prolonged' by opening a whole concave region of the curve that stretches to another point of inflection where a new convex region begins. All the sub-inflection points of our infinitely varying surface are 'condensed' into this region, defined simultaneously by the continuity of the curve through these inflection points and its center of curvature, which we can use to grasp the region as a whole. The idea of "prolonging" a singularity over a set of ordinary points can sound completely bizarre if we forget the metaphor of the folded curve. The whole point is that for Leibniz, the curve never bifurcates. There is a single, best, curve of the world.
The condensation or weaving of continuity here is a type of folding that brings distant parts of the curve into proximity with one another. It thus creates a sort of neighborhood or district or department or quartier (as Deleuze actually calls it). The monad includes the entire world, but it only clearly expresses a certain region of it. The fact that the closure of the monad only happens "at infinity" seems to stretch our metaphor a bit until we realize that the fractal nature of the curve gives it a peculiar elasticity of sorts. We might imagine that any fold tugs on the entire length of curve, but that the effect is felt more clearly in some places than others. This neighborhood is the seed of the body. The particular position of the fold distinguishes one monad from the next and orders the whole curve from a certain perspective.
But how exactly can this work? Should we think of all the singularities included in the department as parts of the monad? What then of all the other singularities of the world that the monad also includes, but only confusedly or obscurely, because they fall outside its department? In the end, it seems that all monads would have the same parts, and differ only in their ordering of them. And without an immanent principle of ordering, we would have to rely on a transcendent God to select each and every monad as suitable for this world.
In fact, I think it's possible that this is what Leibniz actually thought. Deleuze, however, rejects the idea that a monad has extensive parts. He has a very precise notion of how the primitive singularities enter into relation so that they condense into an individual monad. They enter into differential relations, and not relations of part to whole.
In truth, Leibniz never fails to specify that the relation of the minute perception to the conscious perception is not a relation of part to whole, but rather a relation of the ordinary to the remarkable or notable. "Anything which is remarkable must be made up of parts which are not." We have to understand literally—that is, mathematically—that a conscious perception is produced when at least two heterogeneous parts enter into a differential relation that determines a singularity. It is like the equation of the circumference in general, ydy + xdx = 0, in which dy/dx = -x/y expresses a determinable magnitude. (F, 113)
Whenever Deleuze claims that Leibniz "never fails" to express himself in a consistent way, we can be sure that there is enough ambiguity in the original texts to support either reading. So I would attribute this primacy of differential relations to a "possible Leibniz". Regardless, this is such a key difference that I want to really examine it in depth. Differential relations are right at the core of Deleuze's philosophy, which always takes difference rather than identity as its smallest unit. In this case, the smallest units, the primitive singularities, are points of inflection. These are precisely not 'things', but variations, infinitesimals, differentials. The smallest thing in this philosophy is a unit of change. And Deleuze's world is nothing but these points of inflection, this sea of tiny differences that constitute the horizon of being.
The undulating sea of differentials, the collection of all points of inflection or ideal events, the transcendental field, in short, the world, in some sense precedes the condensation of the monad (though it can only be actualized wthin a monad). It nevertheless supports the stable form or convergent neighborhood of the monad. This is not because the differences are assembled into a form the way bricks are assembled into a house. Instead, form is produced through the limit of a differential relation. The analogy here is Leibniz's study of the derivative at a point. The terms dx and dy 'vanish', and yet there remains a determinate relation between them. There is a sort of correlation of difference or a co-relation of variations. This is why Deleuze characterizes the differential relation as selective or perceptive and tells us that it is a relation of ordinary to remarkable. In this infinite differential sea, only certain variations enter into determinate relations, while most others remain simple unrelated disparates. These relations constitute the continuity of change over a particular region of the curve, or what we would now call its differentiablity. The neighborhood of the individual monad is defined by the differentials (primitive singularities) that enter into a relationship with a determinate limit. Not a limit in the sense of an externally bounded form with a certain essential shape, but an internal limit of related differentials. These relations create a structure in the differential field that we can summarize with a topological singularity -- the point of view. Notice here how the meaning of "singularity" has shifted. The primitive singularities or points of inflection give way to the singularity of the center of curvature of the monad's neighborhood. In between, we pass from one primitive singularity to another by prolonging each point of inflection till it connects up continuously with a new one, weaving together a compossible world or line of continuous variation.
What interests us here is less the development of the theory of the idea than the different meanings of the singular. We have encountered three meanings of the singular: the singularity is first of all the inflection, the point of inflexion that is prolonged to the neighborhood of other singularities, thereby constituting lines of the universe in accordance with relations of distance; and then it is the center of the curve on the concave side, insofar as it defines the point of view of the monad in accordance with relations of perspective; finally, it is the remarkable, in accordance with the differential relations that constitute perception in the monad. (F, 117)
So every monad includes every tiny inflection, but for each monad, only some of these differentials relate to others. These relations introduce finite limits into what is otherwise infinite. These differential limits that are like phase transitions of condensation or folding. Each contains a potential 'passage to infinity', as it were but actualized in a determinate fashion.
So far, we have been discussing how to make a definite monad from a sea of difference -- how to fold the fabric of the world into a determinate shape. But the world outside the monad is not a given in this philosophy. It can only be constructed through the process of weaving together the monads produced by this mechanism of condensation. There's obviously a sort of circular logic to the scheme -- the fabric only holds together because it can be folded, and it can only be folded because it holds together. For most of this discussion, we've mostly occupied the God's eye point of view that sees the unfolded and unordered world. But, in actuality, all of this folding occurs entirely internally in the monad which contains this whole world as an already ordered set. From the monad's point of view, variations enter or leave its region. They cross a threshold and enter into its constitutive differential relations. As we've seen though, these aren't the attributes of a fixed monad, but the perceptions of one in motion. Thus the theory of the composite fabrication of the monad from compossible or non-bifurcating singularities is equivalent to a theory of its perceptions. This makes the transition from world to monad equivalent to the transition from unconscious perception to conscious perception.
Deleuze calls this a sort of "hallucinatory perception", since it happens entirely within the monad. Certain relations pop out of the background of tiny variations. These are not external forms or objects that the monad perceives, but the process which constitutes perception in the monad, embedding it in a world it seems to be made for. The complete sea of tiny differentials don't disappear; they subsist within the monad, but without entering into relation. They are the obscure unconscious micro-perceptions which our macro-perceptions condense into a clear form. For Leibniz then, clear perceptions exist along a continuum with obscure micro-perceptions, a continuum with certain thresholds that separate its gradations. And what we call the body of the monad is just that part of the world it perceives clearly, the part that has crossed the threshold into consciousness. Different monads will of course have different thresholds, which allows us to define a sort of evolutionary scale of monads. But in each case the body of the monad is the region that crosses the threshold of perception, the region defined by the limits of certain differential relations.
But if there is a scale of animals, or an "evolution" in the animal series, it exists only to the degree that the differential relations become increasingly numerous, and of an increasingly profound order, determining a zone of clear expression that is not only more vast but also more closed, each of the conscious perceptions that compose it being associated with others in the infinite process of reciprocal determination. These are remembering monads [monades mémorantes]. And even more so, some monads are endowed with the power to extend themselves and to intensify their zone, to attain a veritable connection of their conscious perceptions (and not a simple associative consecution), and to double the clear with the distinct and even the adequate. These are reasonable or reflexive monads ... (F, 118)
Notice though that (so far) this perceived body is still entirely internal to the mind. We began with the world as a pure emission of singularities, a pure virtuality, that condensed into a monad centered on certain of these singularities. Then we approached from the other angle and considered the perceptions of an actualized monad, already defined by certain relations. These were two ways of looking at the same body. In both cases though we are still talking about an ideal realm, albeit one that has now acquired a certain sort of differentiation and is no longer a chaos of difference. The body is a condensation of ideal events or a perception of the monad. In either case it remains immaterial.
This is why we have called the theory of perception "hallucinatory". Because, as far as we know at this point, the monad has no contact with anything outside itself. It's literally making this up. Or perhaps it would be more accurate to say that it is the simultaneous 'making up' of itself and its perceptions. We have called the unconscious micro-perceptions, the differentials of consciousness, that fall outside this region "hallucinatory" because they are tiny variations that don't refer to any concrete external object. But even our conscious macro-perceptions are hallucinatory in this scheme. They too are built from within and condense out of the background of the obscure micro-perceptions. They do not refer to an external object either, but just certain variations entering into a determinate relation. We hallucinate even our own body. Which probably accounts for why it's so much more variable an experience than we like to believe. Meditation shows this to us in a shockingly clear light when it dissolves or changes our image of the body. But in fact it's an everyday occurrence. Get in a car or even put on a hat and you feel 'larger'. Your body image expands to incorporate a new region that suddenly becomes more relevant, more "remarkable", mainly because it can now impede you. Our perceptions are constantly fluctuating between the clear and the obscure, our threshold of consciousness constantly shifting, the edge of our body constantly moving. Deleuze invokes the image of an undulating surface that sometimes crests in great waves that pull everything along in their wake, and sometimes unfolds to an almost glassy stillness.
Fold over folds: such is the status of the two modes of perception, or the two processes—microscopic and macroscopic. This is why the unfold is never the contrary of the fold, but rather the movement that goes from certain folds to other folds. Unfolding sometimes means that I am developing, than I am undoing the infinitely small folds that continually agitate the depth [fond], but in order to outline [tracer] a great fold on the side where forms appear. This is the operation of the waking state [la veille]: I project the world "on the surface of a folding ..." Sometimes, on the contrary, I undo, one by one, the folds of consciousness that pass through all my thresholds, the "twenty-two folds" that surround me and separate me from the depth [fond], in order to discover, in a single movement [d'un coup], this depth of innumerable minute and mobile folds that carry me along at excessive speeds, in the operation of vertigo, like the "enraged charioteer's whiplash ..." I am always unfolding between two folds, and if to perceive means to unfold, then I am always perceiving in the folds. Every perception is hallucinatory because perception has no object. (F, 119)
This theory of hallucinatory perception seems to fit extremely well with the theory of brain architecture various folks have advanced under the broad label of predictive processing. The central idea is that we are never perceiving objects, but only data and its correlations (itself more data). Our perceptions are actually models of the world, simulations based on minimizing the difference between what data we should expect next if the correlations we have seen to date are a reliable guide, and what data actually happen next. To state it more bluntly, we simply guess that these correlations signal the presence of that object. However, while the Bayesian Brain people agree that perception is fundamentally hallucinatory, fundamentally a question of model rather than object, they never seem to really grapple with the question of what makes one physical system count as a model of another. Their use of the term model always seems to invoke a modeling subject who does the guessing and examines the fit. This objection can be waved away with some degree of success by pointing out the nested hierarchical nature of the processing system. But to avoid an infinite regress, we should come back to the idea Deleuze has provided -- a model is a set of differential relations that leads to a limit and thus defines a singularity (even if, in the simplest case, this singularity is a point of inflection that constitutes the continuity of change). This is the definition of monadic perception, and constitutes an immanent definition of a model that never invokes a transcendent subject. All of the order in the world is the spontaneous arising of differential relations.
Hermann Weyl will say that a law of Nature is necessarily a differential equation. (F, 68)
It may seem as if I've gratuitously invoked modern neuroscience and the concept of the model. But it turns out that Weyl's comment is the key to the second phase of Deleuze's "deduction" of the body from the monad. The first phase may entail a monad with structure and perception, but, as he points out, it is still a pure idealism that has not yet left the interior of the monad.
The first stage of the deduction goes from the monad to the perceived. But, precisely, everything seems to stop there, in a kind of Berkeleyan suspense, and nothing authorizes us to conclude from this the presence of a body that would be our own, or the existence of other bodies that might come to affect it. There is only the perceived, internal to the monad, and the phenomenon itself is the perceived. (F, 121)
What we've been calling a body is not yet matter, but still only the folds of the soul. The differentials we've discussed are still the differentials of consciousness, and the thresholds are purely thresholds of awareness. In short, everything is still hallucinatory. We still don't have an answer as to why the monad needs an objective material body, though we have at least explained its need for a subjective spiritual one. The key to this leap is precisely the concept of resemblance, or modeling.
But the true argument is even stranger and more complex: it is that the perceived resembles something, which it forces us to think. (F, 122)
Deleuze points out that resemblance is an easy word to misconstrue in this context. It suggests a definite form one side that 'looks like' a definite form on the other. This is also exactly how we usually use the word "model", as in, the architect made a styrofoam model of the museum. But Weyl's law of nature is a model that looks nothing like nature itself. And Schrondinger's wave equation does not resemble the quantum object we take it to refer to any more than the differential equation of a circle is round. However, the behavior of the differentials in this equation do resemble the differential changes in measurable physical systems -- this fact is what makes it a model and explains why it works as a model. The two sets of differential relations share certain singularities that define a space. In other words, the internal structure of the spiritual resembles the internal structure of the material, even though the two sides look nothing alike. The relationship of resemblance depends on independently extracting corresponding singularities on both sides.
[From what I said earlier, it seems to me that we could add "world/monad" to this list of identities]
Modern science, of course, wants to empirically verify that these particular relations predict the existence of certain macro-perceptions at certain organs. This is how it infers that the "vibrations of matter" resemble the "minute perceptions" of the differentials of consciousness. Leibniz relied instead on divine beneficence. In his scheme, the resemblance is seemingly guaranteed by the very nature of the process of folding. In a fold, one side always "resembles" the other. First, the spiritual differentials fold up, enter into relations, and condense into a monad's more or less conscious point of view on the concave side of the curve. We move from the hypothetical "totally naked monad" (F, 117) to one 'clothed' in a spiritual body. Second, but as a direct consequence or corollary, this folding drags the convex side into a nested set of corresponding folds that precisely fill all the space 'inside' the monad. The two sides match perfectly without ever coming into contact, just as we saw the windowless monads harmonize without interaction. This is the full theory of the fold which is always double. Consider our initial image again in this light. All the "internal" variations of the white side of the curve, the centers of curvature of each of its infinity of sub-units, are perfectly filled by a matching black matter.
We are now in a position to comprehend the entirety of the theory of the fold. The operation of perception constitutes the folds of the soul, the folds that decorate the monad on the inside; but these folds resemble a matter, which must thus be organized in external folds [replis]. We even find ourselves in a quadripartite system of folding, to which the preceding analogy attests, since perception straddles the micro-folds of minute perceptions and the great fold of consciousness, and matter straddles the minute vibratory folds and their amplification on a receiving organ. The folds [plis] in the soul resemble the folds [replis] of matter, and in this way the former direct the latter. (F, 126)
For Leibniz, there is a clear order of deduction which moves from the soul to matter. But in the end, the perfect parallelism diminishes the significance of the starting point. As long as we understand that there is only a single, best, world defined by one continuous curve of variation with an infinity of fractal folds, it doesn't really matter which side we look at. This fractal caveat, however, is the crucial piece that holds all the rest together. The soul of the monad cannot be simple and lacking in internal structure. It must include the whole world and a nested infinity of variations within. And the matter that fills its body cannot be reduced to simple atomic units. It must be "organic" -- infinitely machined and not mechanical.
The error of mechanism is not that it is too artificial to give an account of the living, but that it is not artificial enough, not machinic enough. Our mechanisms are, in effect, composed of parts that are not in turn machines, whereas the organism is infinitely machined, a machine whose parts or pieces are machines, only "transformed by the different folds it receives." (F, 6)
-------------
The idea that, at bottom, there is only infinitesimal difference is the Deleuzian expression of the notion of emptiness. All things are composites, fabrications, constructions. None of them have an essential self-identity. This is true even of the monad, which, as we're seeing, is still a composite structure even though it is the simplest unity. Some time back we actually took this idea that "all A are composed of things that are not A" as the very definition of emptiness. Frequently, however, this way of looking at the world can get snagged on the idea that there must be some smallest element that allows us to avoid an infinite regress. Otherwise it would be turtles all the way down, right?. At first it seems like Deleuze's idea suffers from this same problem. The smallest 'unit' is difference, a differential. And within or behind this difference is more difference. Actually, an infinity of differences. Not a potential infinity though, but an actual infinity -- each unit of difference leads us back to the entire differential field. In a sense, there is a smallest unit, it's just that it is not an element, it's an infinity. Daniel W. Smith makes this point very clearly.
As a way of approaching Ruyer, we might note that Deleuze, in a seminar on Spinoza, had argued that, in the analysis of matter, there are three possibilities for determining what constitutes the "simplest" body: the finite, the indefinite, and the actually infinite. The finite approach, which has inspired atomism since Epicurus and Lucretius, holds that the analysis of matter necessarily reaches a limit, and this limit is the atom or particle (the building block). The indefinite approach, by contrast, insists that, no matter how far the analysis is pushed, the term one arrives at can always in turn by analyzed and divided—in other words, there is no final or ultimate term (indefinite regress). The viewpoint of actual infinity, however, implies a double battle against both the finite and the indefinite. Against the indefinite, it insists that there are indeed ultimate or final terms that can no longer be divided, but against the finite, it insists that these ultimate terms are actually infinite multiplicities that cannot be divided further without changing their nature. In other words, one cannot speak in Spinozistic terms of a simple body as if it were a brick or a building block; rather, the simplest bodies in nature are themselves infinite multiplicities. (From: Raymond Ruyer and the Metaphysics of Absolute Form, 119)
The smallest element is the infinity of inflection points that are folded into every individual monad, and if we try to continue dividing it up into smaller elements we get back the same infinity, but ordered into a different monad. There is no merely potentially infinite, or indeterminate regression. But there is also no atom. There is an infinite regression made actual. This may sound rather bizarre and abstract since we're so unsed to starting any reasoning from the principle of identity. But it's actually not that difficult a thing to experience directly through a meditation technique like self inquiry. There is something that really happens to your experience when you "observe the observer". You don't actually get stuck in the infinite logical loop this action implies (given the impossibility of solving the halting problem, does this constitute proof that you are not a logical machine?). Instead, some new dimension opens up. Something "remarkable".

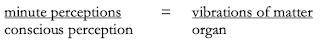
No comments:
Post a Comment