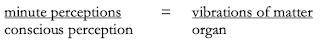The Depths of the Surface

Last time we finally reached Deleuze's articulation of the full fold.  The soul is folded and matter is folded and the two sides are folded together into a single world which the soul in-folds and matter un-folds.  The concept of "resemblance" served as a hinge that carried us from one side to the other because.  The folds of matter are completely separate from the folds of the soul, and yet they resemble one another because of their pre-established harmony.  Consider again the fractal curve that illustrates the fold -- each in-curve of one side is perfectly matched by an out-curve of the other in smaller and smaller details to infinity.  While the distinction between the two sides is completely real, it is nevertheless a consequence of the fact that they are two sides of a single curve.  Recall that resemblance is really nothing more than the differential relations of the folding itself.  Thus the fold is non-dual -- distinction and inseparability go hand in hand.  Matter and the soul are two sides of a single and same world that matter realizes and the soul actualizes.  These operations are distinct, but the bear on the same world.  This explains why Deleuze insists (F, 149) that the sides are two floors of a single house, and not two separate worlds.  The screen or wall or membrane or curve which divides the two floors is contiguous with the rooftop and foundation which holds the whole structure together.  This feature is part of the architecture of the Baroque Fold.  In going to infinity (and in both directions) it brings the sides into such intimate contact that we can hardly tell where one ends and the other begins.  At the limit, they converge to the same world, which can frame both of them only via a "torsion" or topological twist that fuses interior and exterior, and makes the curve cover everything.

I've stated this initial summary in architectural terms because Deleuze begins chapter 8 by returning to a reference he made to Bernard Cache back in chapter 2.  Bear with me though, as this connection is rather winding.

The difference between the two floors is like the difference between a curve of infinite inflection defined immanently (what would be called a mani-fold in two dimensions), and the same curve embedded in an exterior coordinate system.  As we recall from our discussion of Cache, points of inflection are primitive or intrinsic or immanent singularities of a curve.  These do not depend on the orientation of the curve for their definition.  By contrast, the singularities of minimum and maximum of a curve do depend on this embedding -- or framing--  of a curve within a two dimensional coordinate system.  The same curve can be looked at from the inside or the outside.

And yet it is indeed a question of two halves, as we have seen in the case of the infinitesmial calculus. In effect, if we assimilate the object—that is to say, the world—to the primitive equation of a curve with an infinite inflection, we obtain the position or the respective point of view of monads as primitive forces, through a simple rule of tangents (vectors of concavity); from the equation, we can extract differential relations between the minute perceptions that are present in every monad, in such a manner that every monad expresses the entire curve from its point of view. This is thus a first part, a first moment, of the object—the object as perceived, or the world as the expressed. But there still remains the question of knowing what the other part is, which now corresponds to the initial equation: these are no longer pure relations, perception—that is, which concern matter and the bodies that perception resembles. This is the second moment of the object—no longer expression, but content. These are no longer decrees, but the maxims or empirical laws of second Nature. They are no longer singularities of inflection, but singularities of extremum, because the curve is now—and only now—related to coordinates that allow us to determine minima or maxima. (F, 128)

Here Deleuze delivers on the promise he made back on pg. 117 to articulate a fourth type of singularity. 1) Inflection 2) Center of curvature or point of view 3) The 'remarkable' differential relations between micro-perceptions that fill this point of view with various macro-perceptions and 4) Singularities of extrema.  

It's interesting to compare these four singularities to the four classes of beings Deleuze arrived at Back in chapter 4.  I don't think that these should map one-to-one, but there's still some clear parallels.  Back then, it seemed obvious that the monad corresponded to the fourth class of beings -- individuals.  These were closely related to the third class of beings -- things -- because both things and monads were defined by the convergence of an infinite series of differential relations.  In the case of things, this convergence was analogous to the converge of dy/dx to the derivative at a point.  We saw, in that case, that the limit was effectively 'folded into' the point; even though the terms of the series vanished, their relation at a particular point on the curve remained determinate (F, 21).  Later though, we saw Deleuze use a very similar analogy to explain the relation of minute perceptions and conscious perceptions in the monad (F, 113).  In that case, the conscious perceptions that constitute the clear zone inside the monad arise when a set of differentials of consciousness (micro-perceptions) enter into a relation that defines a "remarkable" point or singularity.  These descriptions of the type of convergence of a thing and of a monad's perception are not exactly the same, but they seem to resemble one another.  Especially in the context of the quote above, they're enough to make us wonder whether the third type of singularity -- the "thing" -- is meant to refer to both real objects and objects as actually perceived.  These are the two "moments" of the object or thing.  Are thoughts things?  This in turn suggests that all of the first three singularities could be paired with the first three classes of being and thought of as belonging entirely on the side of the soul or monad, the inside of the curve.  After all, these fall into what Deleuze called the "domain of essences" (F, 73)   Inflections are the primitive or simple singularities which 'condense' into a monad (F, 87), providing it with a point of view that includes not only these particular singularities of inflection but the entire curve (I imagine a Taylor series approximation to a complete function that involves only higher order derivatives at a single point), and within this point of view arise perceptions that select and relate certain differentials that define a singular clear zone.  These internal building blocks of the monad seem to correspond reasonably well to the first three singularities.

Whatever we think of this parallel between things and perceptions, what interests me most here is the the way they both contrast to the type of convergence necessary to define the full monad or fourth class of "unitarily simple" being.  The difference is that the limit which defines the monad itself (as distinct from its perceptions) is exterior to the monad and not localizable within it.  Essentially this limit is the world that all the monads converge to -- the best world.  While we don't want to confuse the two, this is a moment when the monad effectively 'becomes' the whole world, its moment of closure.  In this case, perhaps, the fourth class of beings is as much the world as it is the monad -- or rather it is the completion of the monad through the world, and of the world through the monad.  In a way, these two both lie 'outside' of one another and serve as the convergent limit of one another.  Does this suggest that the world itself is also an example of the fourth type of singularity -- a singularity of extremum? 

It's only at this point that we can come back to our initial idea of framing.  Cache pointed out that it is only the frame which establishes the coordinates for a curve and allows for minima and maxima to be calculated.  The process is like coupling a weightless curve to the force of gravity that operates in a particular direction.  In fact, this seems to be exactly how the monad and the world relate.  The world is the closure of the monad, its exterior limit, and is precisely what allows it to coordinate or harmonize with the other monads.  In short, the world is a frame that the monad passes through to become a complete individual. And this frame is an example of the fourth type of singularity -- the world is singularity of extremum because it is the best possible world. 

It is as if the equation of the world had to be written twice in the form of the two calculi—a first time in the minds that conceive it more or less distinctly, and a second time in a Nature that effectuates it. And no doubt the two calculi implicate and continue each other; they are complementary and must be homogeneized. This is why Leibniz can present the choice between the world and the monads as already operating through a calculus of maximum and minimum. Yet the difference between the two halves subsists, since in one case it is differential relations that determine a maximum of the quantity of being, while in the other case it is the maximum (or minimum) that determines the relations in the equation. We have seen the diversity of singular points in Leibniz: the properties of the extremum indeed governs the constitution of the world chosen in Nature, but the choice itself refers first of all to other properties (of inflection) that bring into play the form of the whole [l'ensemble], at a higher level, as the property of being the limit of a convergent series [suite]. The world, as the great equation, thus has two levels, two moments, or two halves: in the first, it is enveloped or folded in the monads; in the second, it is inserted or refolded into matter. If we confuse the two, the whole system collapses, mathematically no less than metaphysically. On the upper floor, we have a line of variable curvature, without coordinates, a curve with an infinite inflection, whose internal vectors of concavity mark, for each branch, the position of individual monads without mass [en apesanteur]. But it is only in the lower level that we have coordinates that determine the extrema—extrema that define the stability of figures, figures that organize masses, and masses that follow an extrinsic vector of gravity [pesanteur] or the greatest incline. Such is the ogive, [the Gothic arch], which puts symmetry into the inflection, and realizes the figure capable of encountering the minimum of resistance in a fluid. Such is the organization of the Baroque house, with its division into two floors—one made up of weightless individuals, the other of heavy masses [l'un tout en apesanteur individuelle, l'autre en pesanteur de masse]—and the tension between the two, when the first rises or falls (spiritual elevation and physical gravity). (F, 129)

My reading of all these correspondences still feels somewhat speculative to me, but I'm pretty sure about equating Deleuze's World and Cache's Frame, since that is precisely what we need to make sense of this complicated passage.  Because the interesting thing about Cache's frame is that it doesn't close off a space, without opening it up to new possibilities.  It's a strange type of limit that doesn't provide a stopping point without relaunching us.  Deleuze has already argued that this is how Leibniz's best possible world works as well.  Fundamentally, it is not about calculating the maximum of a particular variable, but about maximizing the diversity and continuity of the world as a whole.  Rather than the full curve being given in advance, the world is composed by joining up the singularities in the 'best' way.  This is the odd type of extremum that Deleuze is trying to capture when he insists that there are two types of calculus.  There is indeed a calculus of souls, a 'computation' of the best possible world composed by prolonging a singularity through the series of differential relations associated with it till it converges with the neighborhood of another singularity.  But this is not the same calculus as a calculus of matter, which takes the curve of the world as given, as completely specified and provided with coordinates, and seeks to determine the extremes of certain variables by setting the differential relations equal to zero.  The footnote to the passage above sheds more light on this question.

Insofar as the properties that make the selection possible are the properties of maximum or minimum, they confer on the obtained being an advantage of simplicity and, as it were, an appearance of finality, but this appearance disappears once we realize that what assures the passage to existence is not the fact that the properties in question are extremal properties, but that the selection they determine is implicated in the totality of the structure in question … The exceptional property that distinguishes it is no longer a property of extremum, but the property of being the limit of a convergent series. (F, 129)

So if the best world is a type of extreme, it is a moral extreme that opens the question of what should be optimized, instead of closing this question off by deciding in advance what the important variables are.  The world and the frame can't close the monad, without opening its continuity with other monads.  And, more importantly in this chapter, the world as a singularity of extremum doesn't close the monad without opening matter.  The world is the infinitely nested curve that allows us to pass from the side of the soul to the side of matter.  In fact, as we'll see, it's actually the matter of the world that allows us to pass from monad to monad in its composition.  The real subject of this chapter is this passage from one side of the curve to the other, "a to-and-fro [un va-et-vient]" (F, 150) or what Cache called an oscillation (and related to Simondon's scheme of crystalline individuation).

Before discussing this oscillation though, Deleuze spends some more time sharpening the distinction between the two sides by invoking Ruyer's opposition between "true forms" and "mere aggregates".  The soul knows itself directly and all-at-once, in a state of "self-survey" without distance, as if it were able to achieve a bird's eye view of itself as an absolute domain, one that does not require embedding in a higher dimensional space to be seen as a whole.  It has a trans-spatial and trans-temporal unity, a co-presence to all the parts of itself that Deleuze calls the "distributive" unity of an "every".  The monad is the world in a grain of sand, and every part or moment of the monad is a grain within it that includes the whole monad.  By contrast, matter operates step-by-step, within space and time, and can only be grasped as a whole by some sort of integrating force that stands apart from it or hidden within it.  Which is to say that matter is always an aggregation of separate units or "ones". 

What must be radically distinguished are the folds [replis] of matter, which always consist in hiding something from the relative surface that they affect, and the folds of the form, which on the contrary reveal to itself the detail of an absolute surface, co-present to all its affections. (F, 132)

The ultimate question, however, is how these two radically distinct sides can be related.  We saw part of the story last chapter.  Since the monad contains both clear and obscure regions, it must have a spiritual body constituted by the condensation of obscure perceptions into clear perceptions. In effect, this amounts to a restatement of the fact that soul contains an infinity of folds within it that come together to form one overall fold.  But then, because the structure of perception resembles something (= x), a fact guaranteed by Leibniz's pre-established harmony, we are surprised to discover that the structure internal to the monad must be matched by an external structure that fills it.  The spiritual body of step one therefore has a real counterpart.

The world is a virtuality that is actualized in monads or souls, but it is also a possibility that must be realized in matter or bodies. It is curious, one might object, that the question of reality is posed with respect to bodies which, even if they are not appearances, are simple phenomena. Yet what is a phenomenon, properly speaking, is what is perceived in the monad. When we ask, by virtue of the resemblance of the perceived to something = x, if bodies do not act on each other in such a way that our inner perceptions correspond to them, we are thereby asking the question of a realization of the phenomenon or, better, of a "realizing" of the perceived, that is, of the transformation of the actually perceived world into an objectively real world, an objective Nature. It is not the body that realizes, but it is in the body that something is realized, through which the body itself becomes real or substantial. (F, 133)

So far, so good.  The monad has a body.  And we even know that this body must be organic, in the sense that it is "infinitely machined" (F, 6) with parts that are themselves organisms.  This is the only way for a body to resemble the folds of a soul.  The trouble begins with the fact that this resemblance between the folds of the soul and the folds of matter seems so perfect that it threatens to undermine the radical qualitative distinction between the two sides.  The clear zone of the soul may be a condensation of certain folds, but the monad must nevertheless include the entire world.  It's all at once unity is distributive and trans-spatio-temporal.  So there's not really a sharp dividing line between the stuff inside the monad and the rest of the world; it's all down there somewhere.  But this is not how matter works.  It consists of limited and separated forms that are assembled piece by piece.  There seems to be some tension here between resemblance and belonging.

But what allows us to speak of "the body of a monad" or "its body," since the monad is always an Each, an Every, while the body, always a body, is a One? What grounds the appurtenance of a body to each monad, despite the real distinction and the difference of floors or regimes? It is necessary that a One, without ceasing to be a One, must belong to each Every. (F, 134)

How can a spiritual whole resemble just a material part?  Perhaps we can imagine a pre-established resemblance between the monad and all of matter taken as a whole (see my interpolation in the quote below).  And this seems to be exactly what we need to fill the infinite obscure folds of the soul with "a" body = x.  But this does not sound like a body that belongs to a monad in the sense we normally use this term.  In fact, it would seem that every monad should have the same body in this case; the only body would be the world as a whole.  What then would make this body mine?  This is a question that goes beyond pre-established harmony and asks about the union of body and soul, or the incarnation of a particular soul. 

In brief, the pre-established harmony is distinguished from Malebranche's occasionalism or Spinoza's parallelism not only in itself, but also by its consequences: far from replacing the problem of the union of soul and body, of the incarnation or the "immediate presence," it makes it all the more necessary, even if it is because it allows us to move from the first aspect to the second. In effect, harmony explains the correspondence between each [and every] soul and the [whole] material universe, but when it invokes the correspondence between the soul and its body, it cannot explain it through any relation in the body, because such a relation presupposes a prior belonging or "ownness" [appurtenance] (F, 134)

What follow from this question is a very complicated theory of belonging that centers on an interpretation of one of Leibniz's last and least clear concepts -- the vinculum or substantial link.  I'm not sure how useful the details are here, so I will try to go just deep enough to appreciate the main point -- the curve of the world doesn't allow us to pass from the side of the soul to that of matter without carrying us back and forth across this boundary an infinite number of times.  The more we zoom into the fractal curve, the more complexity we see, and the more rapidly we shuttle back and forth between increasingly tiny crenulations of body and soul.  But something strange happens at this infinite limit, some sort of twist or torsion results in the smallest variations exploding to the size of the whole universe.  We think we are plunging down, but somehow we end up rising all the way back to the surface of the world, just as if the center were nowhere and the periphery everywhere.  Thus this question of belonging, of possessing, which at first seems rather arcane, turns out to be central to the deepest understanding of the fold.  Belonging goes beyond the harmony of two separate floors and takes us to their inseparable union in a single house.

How can a body belong to me?  How can I have a body?  It becomes a strange question if you consider how it inverts the question "who am I?"  For something to belong to me, it can't be me.  Anything that I need to possess can't be essentially mine.  So, while we know I must have a body, I am not identical to that body, and this is why I must posses it.  In short, anything we can lose, we will.  Deleuze includes a brilliant quote from Gabriel Tarde that illustrates this.

"The true opposite of the self is not the non-self, it is the mine; the true opposite of 'to be,' that is, having, is not non-being, but the had." Already in the monad, Leibniz had instituted "I am having diverse thoughts" as the correlate of "I am thinking": perceptions as included predicates, that is, as internal properties, came to replace the attributes. (F, 138)

Much of our discussion has covered things that are intrinsic to the monad -- there's no way it can lose its inflections or point of view or perceptions, ie. any of the first three singularities.  We can say it "possesses" these, but only as internal predicates or definitions, not the way an inert substance possesses attributes.  But the body is external to the monad, and only fills its folds by resemblance (F, 135).  And yet, Deleuze says that the body, while distinct from the monad and outside it, cannot be separated from it.  How do the two stay fixed together if they occupy qualitatively distinct sides that never touch?

We can gain an intuition for how this happens by once again considering the diagram of our curve.  Because it contains the whole world yet is nevertheless finite, the monad must necessarily have both obscure and clear regions within it.  The extent of these domains may grow or shrink, and in fact this is what defines the continuum of monads from rational to "naked", but every monad must contain some of both.  In fact, while the perceptions of the clear region may be consciously denumerable, the obscure region, by its very nature contains a non-denumerable infinity of hidden microperceptions.  No matter how much of the world is unfolded or exposed to our own internal point of view, there will always remain even more of it folded up invisibly inside of us.  In a sense, this is just a restatement of the fact that the fold is an infinite fractal as seen from the concave, or soul, side of the curve.  However, because of a pre-established harmony, the matter which fills this souls must then also be infinitely folded.  In a sense, this is a restatement of the fact that the matter which fills the soul must be 'organic', it must have an infinite nested hierarchy of layers to match the folds of the soul.  Each organism must be filled with and infinity of smaller organism, ad infinitum.  The two sides fit perfectly on an infinity of levels.  Even though they never quite touch, they share the common limit of the world as curve of variation.  

Now, try to imagine pulling these nested fractals two apart.  As soon as the curve of the world becomes a nested fractal, the two sides no longer simply match overall but become stuck to one another like velcro or puzzle pieces.  You can no longer just slide them apart from one another and instead need an extra dimension to disentangle them.  When the fold goes to infinity, we go from harmony, to inseparable union.

How can my monad have an extrinsic possession, outside of itself, on the lower floor? One of Leibniz's essential theses consists in positing both the real distinction and inseparability: it is not because two things are really distinct that they are separable. This is where Harmony and Union discover the principle of their distribution: the pre-established harmony of the soul and the body governs [régit] their real distinction, while union determines their inseparability. (F, 136)

When you fold a nested structure like our curve, you naturally produce a hidden substructure that tends to lock the fold in place, an interesting fact you can investigate with this origami pattern.

From the side of the soul, this nesting corresponds to my unconscious perceptions.  From the side of the body, the nesting corresponds to all of the organic parts and sub-parts -- the organs -- that compose the whole body of my organism.  That is, the details of my organs correspond to the unconscious microperceptions within my organism.  To fulfill the requirements though, these organs must themselves be organic -- they must contain an infinity of sub-organs ad infinitum.  Since we haven't reserved the term monad for human souls alone, each of these organic animal bodies has a corresponding monad of its own.  So the obscure folds inside of me turn out to be the shadows of the other monads needed to compose the world I include and which belong to the hidden organs within my organic body.  I contain multitudes, that is, crowds of other monads, not directly, but through the intermediary of my body.

Leibniz often insists on this point: God does not give the soul a body without furnishing this body with organs. Now what is it that makes a body organic, specific or generic? No doubt, it is made up of infinities of actual material parts, in conformity with infinite division, in conformity with the nature of masses or collections. But these infinities, in turn, would not compose organs if they were not inseparable from crowds of minute monads—monads of heart, liver, knee, eyes, hands (according to their privileged zone that corresponds to one infinity or another): animal monads that themselves belong to the material parts of "my" body, and which should not be confused with the monad to which my body belongs. These are only the requisites of my organic body, specific or generic; and there is no need to ask if matter thinks or perceives, but only whether or not it is separable from these minute souls capable of perception. (F, 136)

This is the process by which a very specific body gets 'stuck' to my monad.  There's now a nesting defined from a particular point of view and not only as a whole, and it's this nesting that makes it impossible to pull what is now my body apart from my soul.  The distributive unity of the soul requires parts that are hidden from it, and which operate like foreign agents embedded within it.  The soul 'possess' matter the way a spirit possess a shaman, but this operation requires another soul to be effective.

Defining "belonging" in this way turns out to have some very weird effects.  My body belongs to me, but its organs actually belong to other monads and not to my monad.  There's an inversion or double directionality of belonging here which forces us to admit that a body belongs to a monad, but every sub-monad belongs to a body.  The tight origami fit of the hierarchy of fractal folding makes us travel back and forth across the curve -- from my soul to its body, but then from the sub-bodies that compose it to their monads, and again from these sub-monads to their bodies, etc ... The direction of belonging flips with each iteration.

We can see, then, that Leibniz's theory of appurtenance brings about a fundamental inversion that will constantly be revived: monads that have a body, to which a body belongs, must be distinguishedfrom monads that are the specific requisites of this body, or which belong to parts of this body. And these second monads, these monads of bodies, themselves have a body that belongs to them, a body specifically other than the body whose requisites they are, and whose parts in turn possess crowds of tertiary monads. And these tertiary monads ...The soul and the body are always really distinct, but inseparability traces a coming-and-going between the  two floors: my unique monad has a body; the parts of this body have crowds of monads; each of these monads has a body…. (F, 136)

Belonging takes us further than harmony.  Its shuttling back and forth across the curve creates an inseparable union of the two sides, almost as if the curve of the world had gained a sort of "thickness" (F, 150) that led to their interpenetration and indiscernibility.  While this resolves the question of how it can be my body, and how I can be immediately present within it without necessarily completely controlling it, it also seems to create major headaches for Leibniz's system.  Because aren't the monads supposed to be completely separate from one another?  Even though they all express the same world, they are not supposed to interact directly, since each already contains everything.  And yet here, somehow, my body is filled with other monads, which are bound to me by what Leibniz calls a vinculum. Am I the only one around here who gives a shit about the rules?

But since no monad contains other monads, domination would remain a vague notion, having only a nominal definition, if Leibniz had not succeeded in defining it precisely by means of a "vinculum substantiale." It is a strange bond, a hook, a yoke, a knot, a complex relation that comprises variable terms and one constant term.
   The constant term will be the dominant monad, since the vincular relation belongs to it or is "fixed" in it. Apparently, we can be all the more astonished that this relation, having as its variable terms other monads (henceforth dominated), cannot be a predicate contained in its subject. That is why the relation will be said to be "substantial," not being a predicate. Since every relation has a subject, the dominant monad is indeed the subject of the vinculum, but it is a subject of "adhesion," not of inherence or inhesion.  This is an almost intolerable paradox in Leibnizianism ... (F, 139)

I don't want to delve into the details of the vinculum beyond what I've already said about the way it carries us back and forth across the curve.  What I find more interesting here is the way this "intolerable paradox" relates to the concept of "torsion" we discussed earlier.  Somehow the closure of the monad is the same as its opening to the continuity of the best world.  What seals it off from all the other monads is paradoxically the same thing that connects it to them as well.  Topologically speaking this paradox can only be resolved through a "twist" like that of a Möbius strip or a Klein bottle, which, unfortunately, makes it impossible to draw the resulting curve in two dimensions.  

... the "unilaterality" of the monad implies, as its condition of closure, a torsion of the world, an infinite fold, which can be unfolded in conformity with the condition only by restoring the other side, not as exterior to the monad, but as the exterior or the outside of its own interiority: a wall [paroi], a supple and adherent membrane, coextensive with the whole inside. Such is the vinculum, the primary and unlocalizable link that lines [borde] the absolute interior. (F, 140)

This is the deepest aspect of the Fold -- it confuses inside and outside and makes it impossible to see exactly what two things are being folded together (F, 150).  I think it also leads us back to the event of the world, "the expressible of all expressions, the realizible of all realizations, the Eventum tantum" (F, 133).  This is the simultaneous closing of all the monads, the completion that requires they pass through the bodies that belong to them and the monads that belong to the bodies' bodies, and ... in an infinitely renewed cycle.  We reach the world by plunging into the infinite series of folds between matter and soul, to the point where we reach a peculiar asymmetric indiscernibility where the curve fills all of space.

Emptying and Filling the Full Fold

I found the opening chapter in Part III, "Having a Body" to be the most interesting one yet.  Part I gives us an initial idea of the concept of the fold and a tangible image to guide us.  The fold is a fractal structure that ends up confusing two topologically distinct sides, just as it would be hard to distinguish the inside and outside of a fabric folded over on itself again and again to produce folds within folds. 

Part II explores the way the fold of the 'concave' or 'spiritual' side can then include an infinity of sub-folds.  This leads us all the way to the central concept of the monad, a spiritual 'unit' that includes or enfolds the whole world.  Given the centrality of the monad in Leibniz's philosophy, we might be tempted to classify it as a type of atomist idealist.  After all, the monad seems to be modeled on the conscious unity of the human subject.  To some extent this is accurate, but we should be aware of the ways in which the marriage of idealism and atomism already produces a unique flavor of both.  Many of the monads are not what we would recognize as minds -- it's not just humans who are monads -- nor are the ones we would recognize treated as purely simple structures without an interior -- in contrast to the atom, the monad has an infinitely nested interiority.  Still, the natural question for any flavor of idealism is why it seems like we also have a body.  If the substance of reality is ideal or spiritual, does this make the body an illusion, a mere appearance?  Why do we need a body at all?

In Part III, Deleuze answers this question beautifully and profoundly, in a way that leads him to a full expression of the concept of the fold in the final pages of the chapter.  The short version is that the structure of Leibniz's peculiar idealism, with its infinitely folded units, drags the body along with it, almost as a byproduct.  Once Leibniz delves into the folds of the soul, he cannot stop there but is forced to keep going.  

The whole question is one of knowing whether, in assuming the force to engender the perceived and the unity of the perceived in the monad, Leibniz does not also assume the force to engender bodies outside of the monads, and outside of their perceptions. (F, 122)

The spiritual folds within folds of the concave side are necessarily 'filled' by the matter of the convex side.  There is only one fold, but it must always have two sides which match or correspond to one another and move together in perfect synchrony.  The fractal enfolding of the spirit is the same action as the infinite infolding of matter, the push of one matched by the pull of the other.  In a sense, we might consider this the Leibnizian version of Spinoza's mind-body parallelism, even though the image is completely different.  Here the two sides are completely inter-penetrated, each following every baroque inflection of the other's curve. But they never touch.  

As you might suspect, the long version is quite a bit longer.  Deleuze phrases the whole thing as "deduction" of why the monad requires a body.  So the starting point is the detailed understanding of the monad that he developed in chapter 5.  There, we saw that the monad was a composition of a set of primitive singularities or ideal events -- predicates not attributes.  We should note that this simple starting point already hides a dizzying complexity.  Monads are unities, but they are not simple or without 'parts'.  They presuppose the world as a "pure emission of singularities" including the particular primitive singularities from which they are built or which they condense.  Here, to give an example, are the singularities of the biblical Adam.

There is an antecedence of the world in relation to the monads, even though a world does not exist outside the monads that express it. But God does not first of all create Adam, even if he makes him sin, or perceives [s'apercevoir] that he will sin: he creates the world in which Adam sins, and includes in the world all the individuals that express it (Sextus raping Lucretia, Caesar crossing the Rubicon ...). We start from the world as a series of inflections or events: it is a pure emission of singularities. Here, for example, are three singularities: to be the first man, to live in a garden of paradise, to have a woman emerge from one's side. And then a fourth singularity: to sin. Such singularities-events are in relation with "ordinary" or "regular" points (the difference here matters little). A singularity is surrounded by a cloud of ordinaries or regulars. (F, 83)

We presume that, in each case, a singularity can be prolonged to the neighborhood of other singularities, along regular lines that have common values in both directions. But here is a fifth singularity: to resist the temptation. It is not simply that this singularity contradicts the fourth one, "to sin," such that a choice must be made between the two. It is rather that the lines of prolongation that go from this fifth point to the three others are not convergent, that is, they do not pass through common values: it is not the same garden, nor the same primeval world [priméité], nor the same gynegenesis. There is a bifurcation. (F, 84)

But at the same time, these other singularities are nothing but the traces of other monads that compose the same compossible world.  The world does not actually exist as a thing in itself outside the monads.  But the monads are all made by God for this single convergent world.  The world is woven of monads, but each thread in the fabric contains all the others as strands within it.  As with Indra's Net, every thing is everything.

Everything is connected, but not in any order.  Each monad includes the entire world, but ordered according to a particular point of view.  It contains all the singularities that the world emits, but it only condenses a certain subset of these.  Their relation constitutes the defining characteristic that makes each monad a distinguishable individual despite the fact that they all include the same world in its entirety.  The joining of this particular set of primitive singularities into a continuity is what Deleuze calls their "condensation" (to refer to the idea of a phase transition which lurks beneath the surface here).  Each singularity is a point capable of being prolonged to the neighborhood of another singular point in precisely the way a point of inflection is 'prolonged' by opening a whole concave region of the curve that stretches to another point of inflection where a new convex region begins.  All the sub-inflection points of our infinitely varying surface are 'condensed' into this region, defined simultaneously by the continuity of the curve through these inflection points and its center of curvature, which we can use to grasp the region as a whole.  The idea of "prolonging" a singularity over a set of ordinary points can sound completely bizarre if we forget the metaphor of the folded curve.  The whole point is that for Leibniz, the curve never bifurcates.  There is a single, best, curve of the world. 

The condensation or weaving of continuity here is a type of folding that brings distant parts of the curve into proximity with one another. It thus creates a sort of neighborhood or district or department or quartier (as Deleuze actually calls it).  The monad includes the entire world, but it only clearly expresses a certain region of it.  The fact that the closure of the monad only happens "at infinity" seems to stretch our metaphor a bit until we realize that the fractal nature of the curve gives it a peculiar elasticity of sorts.  We might imagine that any fold tugs on the entire length of curve, but that the effect is felt more clearly in some places than others.  This neighborhood is the seed of the body.  The particular position of the fold distinguishes one monad from the next and orders the whole curve from a certain perspective.  

But how exactly can this work?  Should we think of all the singularities included in the department as parts of the monad?  What then of all the other singularities of the world that the monad also includes, but only confusedly or obscurely, because they fall outside its department?  In the end, it seems that all monads would have the same parts, and differ only in their ordering of them.  And without an immanent principle of ordering, we would have to rely on a transcendent God to select each and every monad as suitable for this world. 

In fact, I think it's possible that this is what Leibniz actually thought.  Deleuze, however, rejects the idea that a monad has extensive parts.  He has a very precise notion of how the primitive singularities enter into relation so that they condense into an individual monad.  They enter into differential relations, and not relations of part to whole. 

In truth, Leibniz never fails to specify that the relation of the minute perception to the conscious perception is not a relation of part to whole, but rather a relation of the ordinary to the remarkable or notable. "Anything which is remarkable must be made up of parts which are not."  We have to understand literally—that is, mathematically—that a conscious perception is produced when at least two heterogeneous parts enter into a differential relation that determines a singularity. It is like the equation of the circumference in general, ydy + xdx = 0, in which dy/dx = -x/y expresses a determinable magnitude. (F, 113)

Whenever Deleuze claims that Leibniz "never fails" to express himself in a consistent way, we can be sure that there is enough ambiguity in the original texts to support either reading.  So I would attribute this primacy of differential relations to a "possible Leibniz".  Regardless, this is such a key difference that I want to really examine it in depth.  Differential relations are right at the core of Deleuze's philosophy, which always takes difference rather than identity as its smallest unit.  In this case, the smallest units, the primitive singularities, are points of inflection.  These are precisely not 'things', but variations, infinitesimals, differentials.  The smallest thing in this philosophy is a unit of change.  And Deleuze's world is nothing but these points of inflection, this sea of tiny differences that constitute the horizon of being. 

The undulating sea of differentials, the collection of all points of inflection or ideal events, the transcendental field, in short, the world, in some sense precedes the condensation of the monad (though it can only be actualized wthin a monad). It nevertheless supports the stable form or convergent neighborhood of the monad.  This is not because the differences are assembled into a form the way bricks are assembled into a house.  Instead, form is produced through the limit of a differential relation.  The analogy here is Leibniz's study of the derivative at a point.  The terms dx and dy 'vanish', and yet there remains a determinate relation between them.  There is a sort of correlation of difference or a co-relation of variations.  This is why Deleuze characterizes the differential relation as selective or perceptive and tells us that it is a relation of ordinary to remarkable.  In this infinite differential sea, only certain variations enter into determinate relations, while most others remain simple unrelated disparates.  These relations constitute the continuity of change over a particular region of the curve, or what we would now call its differentiablity.  The neighborhood of the individual monad is defined by the differentials (primitive singularities) that enter into a relationship with a determinate limit.  Not a limit in the sense of an externally bounded form with a certain essential shape, but an internal limit of related differentials.  These relations create a structure in the differential field that we can summarize with a topological singularity -- the point of view.  Notice here how the meaning of "singularity" has shifted.  The primitive singularities or points of inflection give way to the singularity of the center of curvature of the monad's neighborhood.  In between, we pass from one primitive singularity to another by prolonging each point of inflection till it connects up continuously with a new one, weaving together a compossible world or line of continuous variation.  

What interests us here is less the development of the theory of the idea than the different meanings of the singular. We have encountered three meanings of the singular: the singularity is first of all the inflection, the point of inflexion that is prolonged to the neighborhood of other singularities, thereby constituting lines of the universe in accordance with relations of distance; and then it is the center of the curve on the concave side, insofar as it defines the point of view of the monad in accordance with relations of perspective; finally, it is the remarkable, in accordance with the differential relations that constitute perception in the monad. (F, 117)

So every monad includes every tiny inflection, but for each monad, only some of these differentials relate to others.  These relations introduce finite limits into what is otherwise infinite.  These differential limits that are like phase transitions of condensation or folding.  Each contains a potential 'passage to infinity', as it were but actualized in a determinate fashion.

So far, we have been discussing how to make a definite monad from a sea of difference -- how to fold the fabric of the world into a determinate shape.  But the world outside the monad is not a given in this philosophy.  It can only be constructed through the process of weaving together the monads produced by this mechanism of condensation.  There's obviously a sort of circular logic to the scheme -- the fabric only holds together because it can be folded, and it can only be folded because it holds together.  For most of this discussion, we've mostly occupied the God's eye point of view that sees the unfolded and unordered world.  But, in actuality, all of this folding occurs entirely internally in the monad which contains this whole world as an already ordered set.  From the monad's point of view, variations enter or leave its region. They cross a threshold and enter into its constitutive differential relations.  As we've seen though, these aren't the attributes of a fixed monad, but the perceptions of one in motion.  Thus the theory of the composite fabrication of the monad from compossible or non-bifurcating singularities is equivalent to a theory of its perceptions.  This makes the transition from world to monad equivalent to the transition from unconscious perception to conscious perception.

Deleuze calls this a sort of "hallucinatory perception", since it happens entirely within the monad.  Certain relations pop out of the background of tiny variations.  These are not external forms or objects that the monad perceives, but the process which constitutes perception in the monad, embedding it in a world it seems to be made for.  The complete sea of tiny differentials don't disappear; they subsist within the monad, but without entering into relation.  They are the obscure unconscious micro-perceptions which our macro-perceptions condense into a clear form.  For Leibniz then, clear perceptions exist along a continuum with obscure micro-perceptions, a continuum with certain thresholds that separate its gradations.  And what we call the body of the monad is just that part of the world it perceives clearly, the part that has crossed the threshold into consciousness.  Different monads will of course have different thresholds, which allows us to define a sort of evolutionary scale of monads.  But in each case the body of the monad is the region that crosses the threshold of perception, the region defined by the limits of certain differential relations. 

But if there is a scale of animals, or an "evolution" in the animal series, it exists only to the degree that the differential relations become increasingly numerous, and of an increasingly profound order, determining a zone of clear expression that is not only more vast but also more closed, each of the conscious perceptions that compose it being associated with others in the infinite process of reciprocal determination. These are remembering monads [monades mémorantes]. And even more so, some monads are endowed with the power to extend themselves and to intensify their zone, to attain a veritable connection of their conscious perceptions (and not a simple associative consecution), and to double the clear with the distinct and even the adequate. These are reasonable or reflexive monads ... (F, 118)

Notice though that (so far) this perceived body is still entirely internal to the mind.  We began with the world as a pure emission of singularities, a pure virtuality, that condensed into a monad centered on certain of these singularities.  Then we approached from the other angle and considered the perceptions of an actualized monad, already defined by certain relations.  These were two ways of looking at the same body.  In both cases though we are still talking about an ideal realm, albeit one that has now acquired a certain sort of differentiation and is no longer a chaos of difference.  The body is a condensation of ideal events or a perception of the monad.  In either case it remains immaterial.  

This is why we have called the theory of perception "hallucinatory".  Because, as far as we know at this point, the monad has no contact with anything outside itself.  It's literally making this up.  Or perhaps it would be more accurate to say that it is the simultaneous 'making up' of itself and its perceptions.  We have called the unconscious micro-perceptions, the differentials of consciousness, that fall outside this region "hallucinatory" because they are tiny variations that don't refer to any concrete external object.  But even our conscious macro-perceptions are hallucinatory in this scheme.  They too are built from within and condense out of the background of the obscure micro-perceptions.  They do not refer to an external object either, but just certain variations entering into a determinate relation.  We hallucinate even our own body.  Which probably accounts for why it's so much more variable an experience than we like to believe.  Meditation shows this to us in a shockingly clear light when it dissolves or changes our image of the body.  But in fact it's an everyday occurrence.  Get in a car or even put on a hat and you feel 'larger'.  Your body image expands to incorporate a new region that suddenly becomes more relevant, more "remarkable", mainly because it can now impede you.  Our perceptions are constantly fluctuating between the clear and the obscure, our threshold of consciousness constantly shifting, the edge of our body constantly moving.  Deleuze invokes the image of an undulating surface that sometimes crests in great waves that pull everything along in their wake, and sometimes unfolds to an almost glassy stillness.

Fold over folds: such is the status of the two modes of perception, or the two processes—microscopic and macroscopic. This is why the unfold is never the contrary of the fold, but rather the movement that goes from certain folds to other folds. Unfolding sometimes means that I am developing, than I am undoing the infinitely small folds that continually agitate the depth [fond], but in order to outline [tracer] a great fold on the side where forms appear. This is the operation of the waking state [la veille]: I project the world "on the surface of a folding ..." Sometimes, on the contrary, I undo, one by one, the folds of consciousness that pass through all my thresholds, the "twenty-two folds" that surround me and separate me from the depth [fond], in order to discover, in a single movement [d'un coup], this depth of innumerable minute and mobile folds that carry me along at excessive speeds, in the operation of vertigo, like the "enraged charioteer's whiplash ..." I am always unfolding between two folds, and if to perceive means to unfold, then I am always perceiving in the folds. Every perception is hallucinatory because perception has no object. (F, 119)

This theory of hallucinatory perception seems to fit extremely well with the theory of brain architecture various folks have advanced under the broad label of predictive processing.  The central idea is that we are never perceiving objects, but only data and its correlations (itself more data).  Our perceptions are actually models of the world, simulations based on minimizing the difference between what data we should expect next if the correlations we have seen to date are a reliable guide, and what data actually happen next.  To state it more bluntly, we simply guess that these correlations signal the presence of that object.  However, while the Bayesian Brain people agree that perception is fundamentally hallucinatory, fundamentally a question of model rather than object, they never seem to really grapple with the question of what makes one physical system count as a model of another.  Their use of the term model always seems to invoke a modeling subject who does the guessing and examines the fit.  This objection can be waved away with some degree of success by pointing out the nested hierarchical nature of the processing system.  But to avoid an infinite regress, we should come back to the idea Deleuze has provided -- a model is a set of differential relations that leads to a limit and thus defines a singularity (even if, in the simplest case, this singularity is a point of inflection that constitutes the continuity of change).  This is the definition of monadic perception, and constitutes an immanent definition of a model that never invokes a transcendent subject.  All of the order in the world is the spontaneous arising of differential relations.  

Hermann Weyl will say that a law of Nature is necessarily a differential equation. (F, 68)

It may seem as if I've gratuitously invoked modern neuroscience and the concept of the model.  But it turns out that Weyl's comment is the key to the second phase of Deleuze's "deduction" of the body from the monad.  The first phase may entail a monad with structure and perception, but, as he points out, it is still a pure idealism that has not yet left the interior of the monad.

The first stage of the deduction goes from the monad to the perceived. But, precisely, everything seems to stop there, in a kind of Berkeleyan suspense, and nothing authorizes us to conclude from this the presence of a body that would be our own, or the existence of other bodies that might come to affect it. There is only the perceived, internal to the monad, and the phenomenon itself is the perceived. (F, 121)

What we've been calling a body is not yet matter, but still only the folds of the soul. The differentials we've discussed are still the differentials of consciousness, and the thresholds are purely thresholds of awareness.  In short, everything is still hallucinatory.  We still don't have an answer as to why the monad needs an objective material body, though we have at least explained its need for a subjective spiritual one.  The key to this leap is precisely the concept of resemblance, or modeling.  

But the true argument is even stranger and more complex: it is that the perceived resembles something, which it forces us to think. (F, 122)

Deleuze points out that resemblance is an easy word to misconstrue in this context.  It suggests a definite form one side that 'looks like' a definite form on the other.  This is also exactly how we usually use the word "model", as in, the architect made a styrofoam model of the museum.  But Weyl's law of nature is a model that looks nothing like nature itself.  And Schrondinger's wave equation does not resemble the quantum object we take it to refer to any more than the differential equation of a circle is round.  However, the behavior of the differentials in this equation do resemble the differential changes in measurable physical systems -- this fact is what makes it a model and explains why it works as a model.  The two sets of differential relations share certain singularities that define a space.  In other words, the internal structure of the spiritual resembles the internal structure of the material, even though the two sides look nothing alike.  The relationship of resemblance depends on independently extracting corresponding singularities on both sides.

[From what I said earlier, it seems to me that we could add "world/monad" to this list of identities]

Modern science, of course, wants to empirically verify that these particular relations predict the existence of certain macro-perceptions at certain organs.  This is how it infers that the "vibrations of matter" resemble the "minute perceptions" of the differentials of consciousness.  Leibniz relied instead on divine beneficence.  In his scheme, the resemblance is seemingly guaranteed by the very nature of the process of folding.  In a fold, one side always "resembles" the other.  First, the spiritual differentials fold up, enter into relations, and condense into a monad's more or less conscious point of view on the concave side of the curve.  We move from the hypothetical "totally naked monad" (F, 117) to one 'clothed' in a spiritual body.  Second, but as a direct consequence or corollary, this folding drags the convex side into a nested set of corresponding folds that precisely fill all the space 'inside' the monad.  The two sides match perfectly without ever coming into contact, just as we saw the windowless monads harmonize without interaction. This is the full theory of the fold which is always double.  Consider our initial image again in this light.  All the "internal" variations of the white side of the curve, the centers of curvature of each of its infinity of sub-units, are perfectly filled by a matching black matter.

We are now in a position to comprehend the entirety of the theory of the fold. The operation of perception constitutes the folds of the soul, the folds that decorate the monad on the inside; but these folds resemble a matter, which must thus be organized in external folds [replis]. We even find ourselves in a quadripartite system of folding, to which the preceding analogy attests, since perception straddles the micro-folds of minute perceptions and the great fold of consciousness, and matter straddles the minute vibratory folds and their amplification on a receiving organ. The folds [plis] in the soul resemble the folds [replis] of matter, and in this way the former direct the latter. (F, 126)

For Leibniz, there is a clear order of deduction which moves from the soul to matter.  But in the end, the perfect parallelism diminishes the significance of the starting point.  As long as we understand that there is only a single, best, world defined by one continuous curve of variation with an infinity of fractal folds, it doesn't really matter which side we look at.  This fractal caveat, however, is the crucial piece that holds all the rest together.  The soul of the monad cannot be simple and lacking in internal structure.  It must include the whole world and a nested infinity of variations within.  And the matter that fills its body cannot be reduced to simple atomic units.  It must be "organic" -- infinitely machined and not mechanical. 

The error of mechanism is not that it is too artificial to give an account of the living, but that it is not artificial enough, not machinic enough. Our mechanisms are, in effect, composed of parts that are not in turn machines, whereas the organism is infinitely machined, a machine whose parts or pieces are machines, only "transformed by the different folds it receives." (F, 6)

-------------

The idea that, at bottom, there is only infinitesimal difference is the Deleuzian expression of the notion of emptiness.  All things are composites, fabrications, constructions.  None of them have an essential self-identity.  This is true even of the monad, which, as we're seeing, is still a composite structure even though it is the simplest unity.  Some time back we actually took this idea that "all A are composed of things that are not A" as the very definition of emptiness.  Frequently, however, this way of looking at the world can get snagged on the idea that there must be some smallest element that allows us to avoid an infinite regress.  Otherwise it would be turtles all the way down, right?.  At first it seems like Deleuze's idea suffers from this same problem.  The smallest 'unit' is difference, a differential.  And within or behind this difference is more difference.  Actually, an infinity of differences.  Not a potential infinity though, but an actual infinity -- each unit of difference leads us back to the entire differential field.  In a sense, there is a smallest unit, it's just that it is not an element, it's an infinity.  Daniel W. Smith makes this point very clearly.

As a way of approaching Ruyer, we might note that Deleuze, in a seminar on Spinoza, had argued that, in the analysis of matter, there are three possibilities for determining what constitutes the "simplest" body: the finite, the indefinite, and the actually infinite. The finite approach, which has inspired atomism since Epicurus and Lucretius, holds that the analysis of matter necessarily reaches a limit, and this limit is the atom or particle (the building block). The indefinite approach, by contrast, insists that, no matter how far the analysis is pushed, the term one arrives at can always in turn by analyzed and divided—in other words, there is no final or ultimate term (indefinite regress). The viewpoint of actual infinity, however, implies a double battle against both the finite and the indefinite. Against the indefinite, it insists that there are indeed ultimate or final terms that can no longer be divided, but against the finite, it insists that these ultimate terms are actually infinite multiplicities that cannot be divided further without changing their nature. In other words, one cannot speak in Spinozistic terms of a simple body as if it were a brick or a building block; rather, the simplest bodies in nature are themselves infinite multiplicities. (From: Raymond Ruyer and the Metaphysics of Absolute Form, 119)

The smallest element is the infinity of inflection points that are folded into every individual monad, and if we try to continue dividing it up into smaller elements we get back the same infinity, but ordered into a different monad.  There is no merely potentially infinite, or indeterminate regression.  But there is also no atom.  There is an infinite regression made actual.  This may sound rather bizarre and abstract since we're so unsed to starting any reasoning from the principle of identity.  But it's actually not that difficult a thing to experience directly through a meditation technique like self inquiry.  There is something that really happens to your experience when you "observe the observer".  You don't actually get stuck in the infinite logical loop this action implies (given the impossibility of solving the halting problem, does this constitute proof that you are not a logical machine?).  Instead, some new dimension opens up. Something "remarkable".